Differential Evolution

Hi! Welcome.

I hope this entry to be kind of different to the first one I made a looong time ago.

I started using vanilla Emacs recenlty, I give thanks to professor Guerra for this. I learned some SBCL during his lectures, and I became amazed of how integrated the coding experience writting Lisp using SLIME is. I come from Julia land where the workflow is heavily based on using the Julia REPL.

Eventually I found myself enjoying more writting Lisp than Julia using their respective workflows, but I really missed Julia's package manager.

Then, due to my itching curiosity, I stumbled upon other lisp-like languages. First I found Clojure, then I found Racket. I first liked Clojure the most because of the build your own products vibe, but quickly became confused in the docs. On the other hand, Racket seemed very very similar to what I already knew. Then, as always, I lost my time reading blog posts on which one to choose or if I should keep up with SBCL instead.

Now I was in the same hole we all get to when learning a new programming language: what project(s) can I do? which tutorials can I follow? and so on... You know how this goes. The neverending days of zero progress, just me and tutorial hole. Oh, and don't forget the imposter syndrome.

I hope Racket perseveres and becomes a thriving language in the future just like I hope the same for Julia, kudos to the communities behind both languages.

The fist function that will be taken as aptitude function is

where $n$ is the number of components of vector $\vec{x}$.

Figure 1. Plot of $F(\vec{x})$.

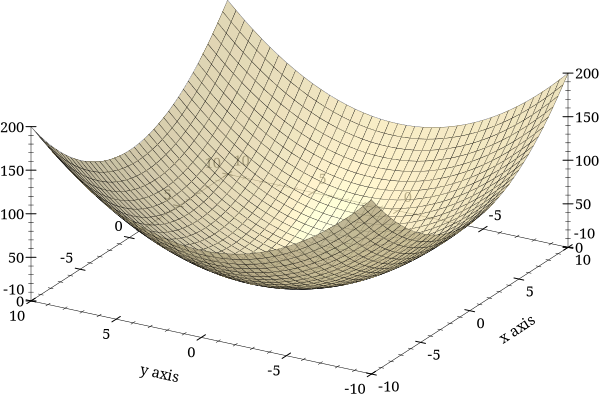
The second function is

Figure 2. Plot of function $G(\vec{x})$.

What is Differential Evolution?

Missing

Hands–on

Before anything else, the following libraries are the ones used for this project.

#lang racket/base

(require racket/list)
(require racket/random)
(require racket/math)
(require plot)

;; Evaluations counter
(define *evals-count* 0)

;; Default number of guests to create mutant list
(define *guests-count* 3)

From the global variables above, the firs one *evals-count* help us to keep track of how many evaluations have been made throughout the algorithm execution, whereas *guests-count* defines the number of solutions that contribute into generating a new mutant vector. Each time one solution is created or a currently existing solution is modified, the evaluation count increases by 1 until a maximum has been reached, it is associated with the action of computing a score to a solution.

Solutions

Before anything else we need a way of representing a solution, one way would be to use association lists or hash tables, these two data structures are readily available in Racket and would allow us to keep the solution itself and a score to know how good the solution is. An alternative is to use Racket's mutable structs with two fields that will contain the aforementioned information such as,

;; Struct to store the relevant information of a solution
(struct solution (slist sscore)
  #:mutable                             ; Makes the struct mutable
  #:transparent)                        ; Allows for field inspection

where the solution itself is stored in slist as a list, and its score in sscore. We still need a proper way to initialize each solution, we do so as

;; Produce a solution with default 'empty fields
(define (make-solution [slist 'empty] [sscore 'empty])
  (set! *evals-count* (add1 *evals-count*))
  (solution slist sscore))

with its available fields initialized to the symbol 'empty to represent that the fields contain no information. Notice that *evals-count* will increase by 1 each time that a new solution is generated!

For example, loading the file into a REPL, and running (make-solution) twice will result in the following behavior:

; --- REPL
> (make-solution)
(solution 'empty 'empty)
> (make-solution)
(solution 'empty 'empty)
> *evals-count*
2

Although, none of the solutions remain stored in the REPL. On the other hand, a solution can be generated directly by creating solution struct as

; --- REPL
> (solution '(1 2 3) 0)
(solution '(1 2 3) 0)
> *evals-count*
2

and this will not increse the evaluation counter as opposed to make-solution.

These solutions are related to $\vec{c}$ which is the argument to both equations, (1) and (2). They depend on a n–dimensional vector $\vec{x}$, and it can be represented as a simple Racket list^[1].

The solutions in Differential Evolution are randomly initialized, meaning that the ith–entry of a solution's slist is a random number, said entry is equivalent to $x_i$ (the ith–coordinate of $\vec{x}$). An easy way to generate a random number for each $x_i$ within a range is

where $l$ and $u$ correspond to the lower and upper limits, respectively, $r$ is a random number sampled between 0 and 1 under a uniform probability distribution.

Racket's random number function random can be used to compute $r$. random generates a random number within range $(0,1)$.

The implementation of eq. (3) can be written directly as

;; Generate an inexact random number within range (inflim,suplim)
(define (random-number inflim suplim)
  (+ inflim
     (* (random)
        (- suplim inflim))))

but the lower and upper limits are never chosen due to the implementation details of random.

;; Generate a list filled up with inexact random numbers within the same 
;; range (inflim,suplim] of length given by lstsize
(define (random-list inflim suplim lstsize [rndlst empty])
  (cond
    [(equal? lstsize 0) rndlst]
    [else (random-list
           inflim
           suplim
           (sub1 lstsize)
           (cons (random-number inflim suplim) rndlst))]))

Initialize Population

Differential evolution works with a population of solutions.